When a personally significant event occurs, human beings often wonder if there is a reason for it or if it is merely a coincidence. Let us call this the two hands of fate, with one hand being called causal, and the other chance. How do we determine which hand of fate we are dealing with?
This article ties together the concepts of probability, coincidence, causality, and an evolutionary concept called exaptation.
Why do we care about fate, chance, and causality?
The two hands of fate have delivered an occurrence.
It could be a potential adverse reaction following a recent vaccination, it could be getting a speeding ticket, it could be a diagnosis of cancer, or it could be that someone in your class has the same birthday. We may have preferences about each of these events. We might wish to either avoid or repeat the occurrence, or to seek justice or help after the event. If the event is entirely a matter of chance, there may be little we can do about it, but if the event has a causal mechanism, we might improve the likelihood of a chosen future through understanding of the cause.
Causal events – the first hand of fate
Some occurrences have obvious causality. For example, speeding while driving, leading to a speeding ticket. Correlation and causality are indisputable. The act of speeding is a necessary condition – that is one must meet this condition for the outcome to be possible – but not a sufficient one.[1]We may not get the ticket even if we speed. There are other variables involved, but speeding is a clear cause.
Many other events in life can be causal, but in a much weaker sense than this speeding example. For example, cancer, which has multiple interacting factors. The effects of genetics, lifestyle, exercise, smoking, and alcohol may be difficult to determine amongst all the other variables, which to some degree act as confounders to the study.[2]Studies often require very large numbers of participants to determine weaker causes such as the effects of moderate drinking on cancer rates.[3]
Coincidences and chance – the surprising second hand of fate
Coincidences are events that are surprising, thought to be meaningful, but not causally related.[4]Coincidences are of great interest to humans, as we are curious beings who tend to try to understand events, though often with a skewed idea of their likelihood.[5]We may wonder if a particular event is by chance, or if it is causal. Evaluating coincidences will help us evaluate weaker causal events.
A ubiquitous example when considering coincidences and probability is the so-called “birthday paradox,” where we consider the chances that there may be two students in a class with the same birthday. It is called a paradox (it is not actually a paradox) because most people have a grossly erroneous assessment of the odds of two coinciding birthdays.[6][7]This general idea will be of no surprise to readers of Brian Russell’s article The numbers game – conquering confusing card quizzes and investigating information theory on the probabilities of playing cards.
Breaking down the birthday paradox – base rates
The odds of two people having different birthdays is 364/365. This is the base rate, and it is based, obviously, on the number of days in the year. It assumes that people are equally likely to be born on any day of the year. The two histograms below show the monthly percentages of births in the United States in 2006 and in Canada between 1991 and 2020, respectively. They vary somewhat, but for the sake of simplicity, we will treat any day of the year as equally probable.
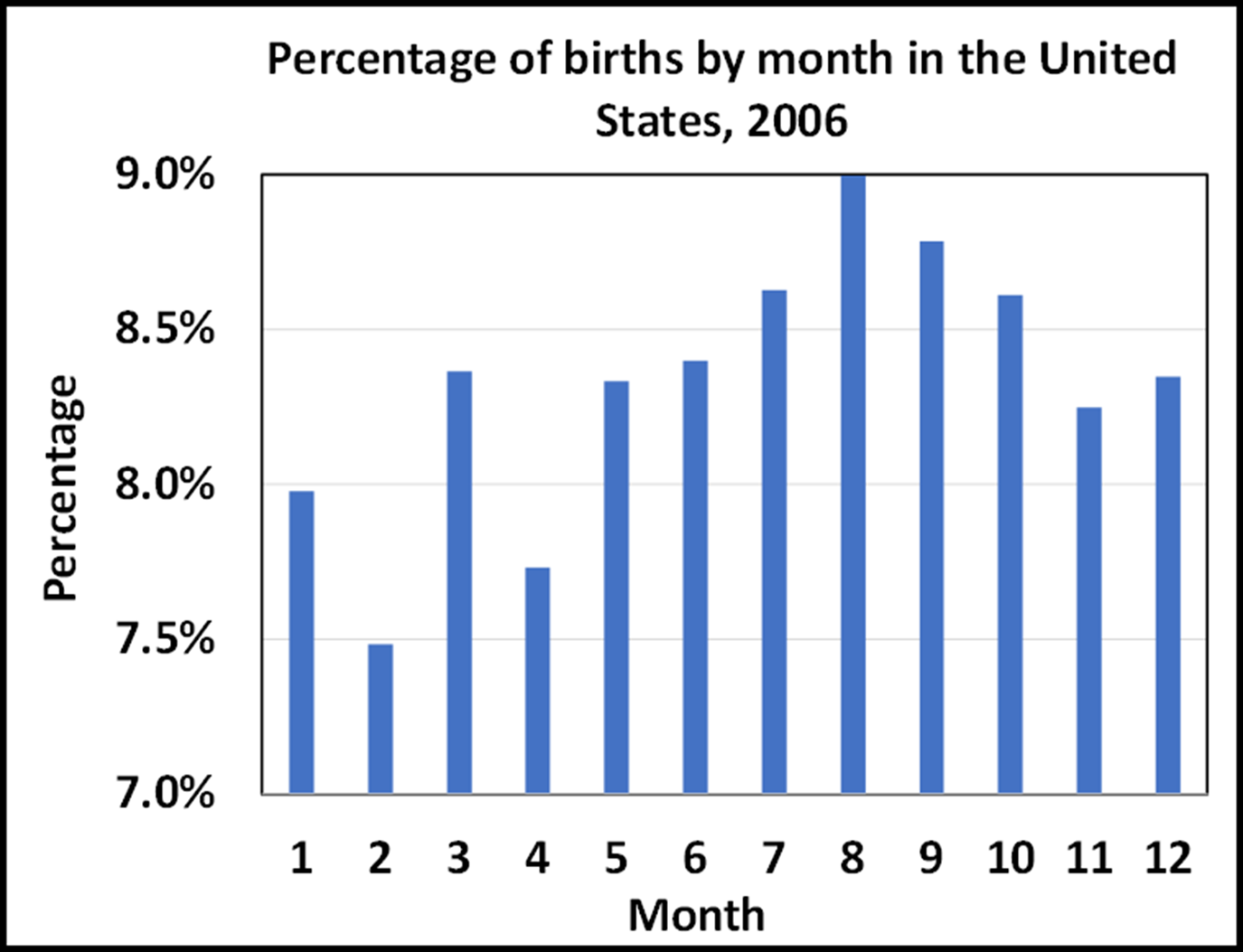
Histogram of the percentages of births by month in the U.S. in 2006. The range is slightly greater than 1.5%.[8]
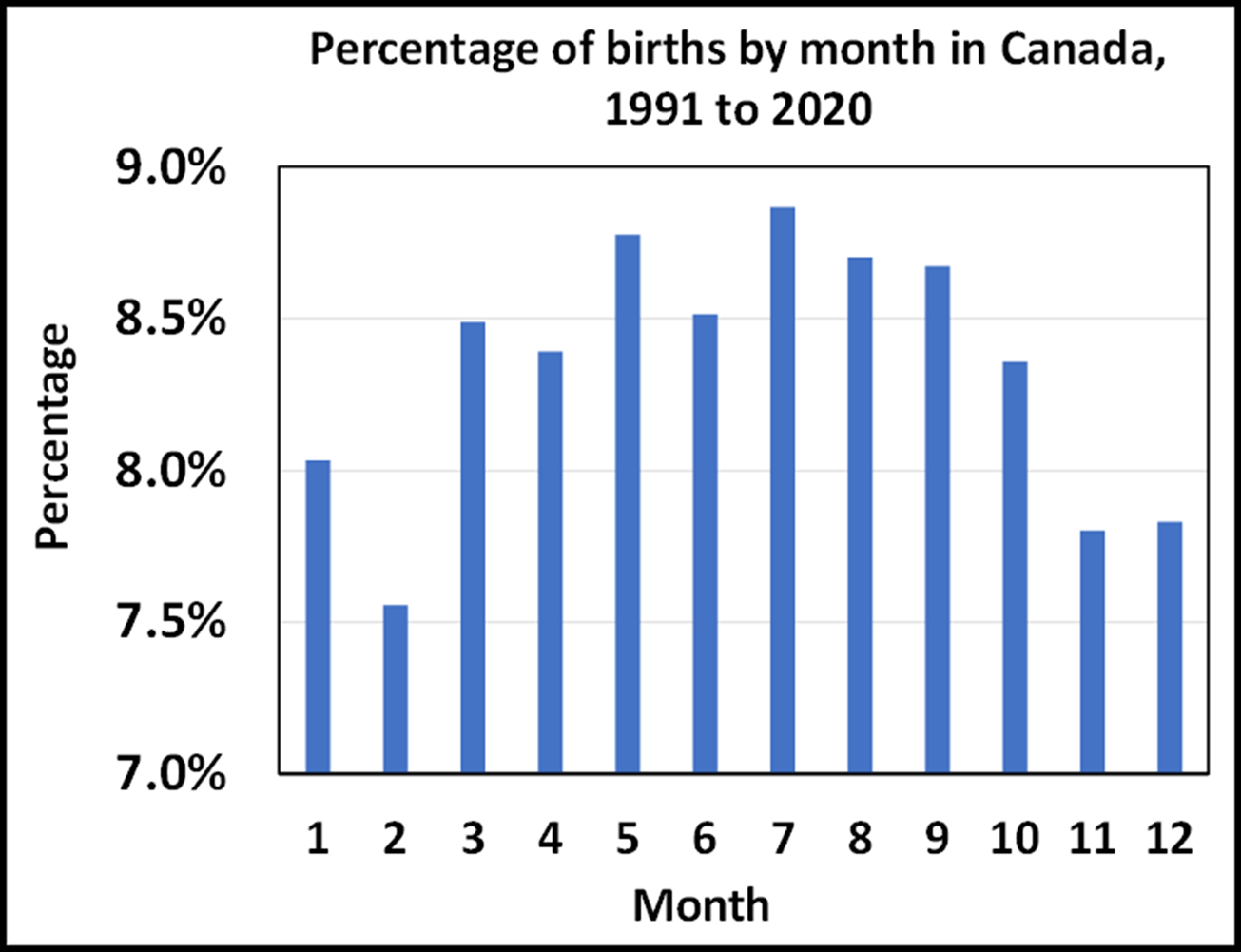
Histogram of the percentages of births by month in Canada from 1991 through 2020. The range of variation by month is slightly less than 1.5%.[9]
With the base rate in hand, we must look at the number of permutations in a classroom. If N is the number of students, we must determine the total number of unique pairs. That number will be:
Permutations = P = (N x (N-1)) / 2 [10]
And the chances of two people in the class having a birthday on the same day becomes:
If we solve this equation for class sizes from zero to 99, we produce the chart below. At a class size of 23, there is about a 50% chance of two people having the same birthday. This low number is surprising to most.
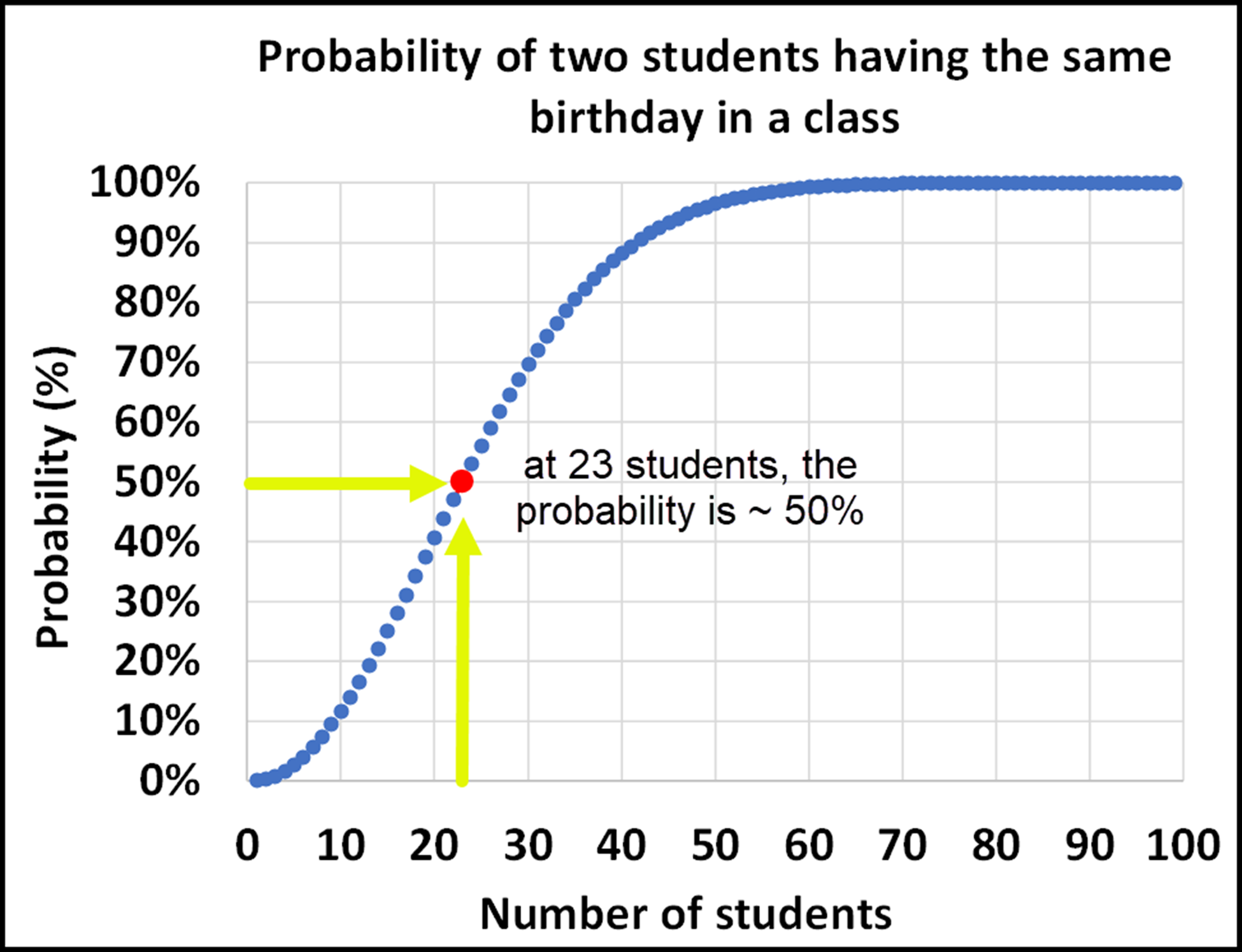
The probability of two students in a class having the same birthday is higher than most people would expect, which is why this is a classic problem in probability and coincidence.
Which hand? Events that may be coincidental or causal
We may reasonably question whether some events are coincidental or causal. Which hand of fate is it? When a negative event occurs after vaccination, the question of causality becomes important, particularly if the event is severe. Most individual case reports of an adverse event following vaccination will have an insufficient amount of evidence to determine causality. The first step in investigating a potential causal link between a vaccine and an adverse event is to compare the base rates of the event type for a large group of subjects with or without vaccination. If the base rates are in excess after vaccination, then further controlled study may be warranted.[12]This will be addressed in a future article.
The third hand of fate – exaptation of mindful positivity
Although it may sometimes be challenging to distinguish the hand of cause from that of coincidence, with enough data and a carefully designed experiment, it is eventually possible to do so. This is important in making policy decisions on both a personal and governmental scale.
But there may be a third hand of fate, and that is how we choose to react to events. In the article In search of the zone on the sharp end, I described the importance of a confidence and a skill – challenge balance in creating flow, an optimal state of performance. Mindset affects performance. In the article When failure is not failure: the rationality of positivity amid catastrophe, we discussed the importance of a positive mindset in happiness, the handling of failure, and in overall success. Evidence in these articles suggests that we may, sometimes, be able to interact with events and through out own agency create something better from them.
This assertion may be seen as aspirational, but let us take an example from evolutionary biology: the concept of exaptation. Famous scientists Stephen Jay Gould and Elizabeth Vrba coined the term to account for mutations that did not immediately increase the fitness of the subject. Feathers on non-flying dinosaurs is a good example. Exaptation is when the animal finds a use for a mutation outside its original role. The dinosaur made the most of its feathers (which evolved for thermoregulation), and learned to fly.[13]
Which is to say, sometimes we must find the most productive use for the events in our lives, be they causal or coincidental. This is not always possible or applicable, but the dinosaurs gave us something to strive for. Make the most of it, make the best of it, learn something from it. Find a reason or make one that makes us better.
The third hand of fate, it turns out, is our own.
References
[1] Hughes, W., J. Lavery, and K. Doran, 2010, Critical Thinking: an Introduction to the Basic Skills, sixth edition: Broadview Press
[2] Stanford Health Care, What Causes Cancer?
[3] Klatsky, Arthur, et al, 2015, Alcohol Intake, Beverage Choice, and Cancer: A Cohort Study in a Larger Kaiser Permanente Population, The Permanente Journal, V 19 N 2, 28-34
[4] Diaconis, Persi and Frederick Mostieller, 1989, Methods for Studying Coincidences, Journal for the American Statistical Association, V 84, N 408, 853-861
[5] Beitman, Bernard, December 16, 2015, The Promised & Problems of Probability in Coincidence Studies: Where Random Meets Meeting, Psychology Today
[6] Better Explained, Understanding the Birthday Paradox
[7] Paulos, John Allen, 1988, Innumeracy: Mathematical Illiteracy and its Consequences: Hill and Wang
[8] Melina, Remy, July 27, 2010, In Which Month Are Most Babies Born? LiveScience.com
[9] Statistics Canada, 2021, Live births, by month
[10] Better Explained, Understanding the Birthday Paradox
[11] Better Explained, Understanding the Birthday Paradox
[12] Halsey, Neal, 2002, The science of evaluation of adverse events associated with vaccination, Seminars in Pediatric Infectious Diseases, V 13, N 3, 205-214
[13] Gould, Stephen and Elisabeth Vrba, 1982, Exaptation—a Missing Term in the Science of Form, Paleobiology, V 8, No 1,4-15
(Lee Hunt – BIG Media Ltd., 2021)


