Several months ago, a friend posted on his Facebook page a math question that he had found on a geophysics blog. I love these kinds of quizzes and since I thought the answer was obvious, I jumped in with my answer. The problem was that my answer was wrong! Another friend of my friend set me straight. Here is the story of my humbling experience:
It took some time to be convinced that I was wrong, but when I finally saw why she had the right answer, it was a good learning experience. First, it taught me to be more humble, and, second, not knowing the answer to a problem gives you the opportunity to learn something new. That is what I like about mathematics over political discussions; there is always a right answer, and you can convince the other person of the correct solution with a reasoned argument. In a political discussion (certainly in Canada and the U.S. these days), both sides are convinced they are right, and no amount of argument will change their minds.
By now, I’m sure you all want to know what the question was! It was this: “A friend draws a card at random from a deck of 52 playing cards and asks you to guess what it is. But before you guess, you can ask one of the following questions, which your friend must answer correctly: is it red, is it a face card, or is it the ace of spades?” As mentioned, I immediately thought I had the answer. I thought you should ask if the card is a red card, the first option, since your odds are now 1/26 instead of 1/52 because half the cards are red. I dismissed the third option immediately by saying it was obviously wrong since the probability of getting the ace of spades correct is only 1/52. I also thought that the second option was incorrect since there are 12 face cards, so 12/52, or 3/13 odds.
However, the truth is that any of the questions would be a good choice since they all reduce your odds of guessing the right answer to 1/26. This is quite non-intuitive. What I had missed is factoring in the yes or no part of the question.
In other words, I had come up with the correct answer to a different question: “If your friend drew a card at random and asked you three questions: is it a red card, is it a face card, or is it the ace of spades, which of your answers has the highest chance of success?” Now, the answer is obviously the first, since you will be right half the time if you guess red, but only 3/13 of the time if you guess it is a face card, and only 1/52 if you guess the card is the ace of spades.
The correct solution to this problem is to realize that by asking one question, you have reduced your odds by adding information, and as you ask a more restricted question, you have increased the certainty of getting that card if the answer is yes, but decreased the certainty if the answer is no. Everything averages out to the same probability – 1/26. For example, let’s take the first question. If your friend answers yes, you have restricted the number of possible cards to 26, which reduces your odds from 1/52 to 1/26. But if your friend answers no, you still have reduced your odds from 1/52 to 1/26. Another way of saying this is that the probability of red times the probability of yes plus the probability of black times the probability of no equals 1/26, which can be written as follows, where the symbol p means probability:
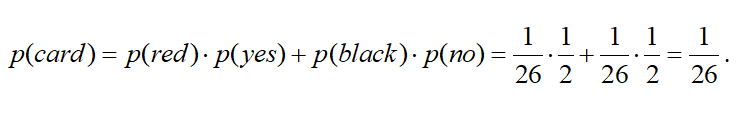
Now let’s look at the face-card scenario in the above notation:
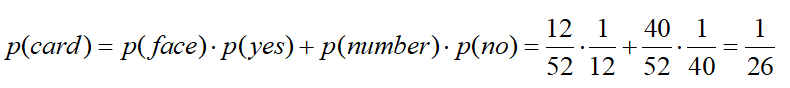
In other words, you have a lower probability of drawing a face card than a number card, but you have a higher probability of correctly predicting which face card you have drawn than which number card you have drawn.
Finally, let’s look at the third option, guessing the ace of spades (a_of_s):
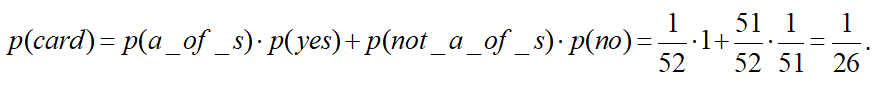
This is saying that you only had a 1/52 chance of guessing the card, but if your guess is correct, your guess has a probability of one. If your guess is wrong, you have a probability of 51/52 that it is not the ace of spades but only a 1/51 probability that you can guess the right card. Notice that all permitted questions result in the same probability of guessing the card correctly.
The solution to this simple card trick is an example of information analysis called “entropy theory”.[1] Entropy refers to the amount of randomness in a system; a high degree of randomness equals high entropy. Entropy theory can apply to everything from molecules to Morse code to the universe.
One application is found in looking at the basic code of life, DNA. When Watson and Crick (1953) published their famous paper on the structure of DNA as a double helix, they were simply talking as biochemists. They showed that each strand of DNA in the double helix is made up exclusively of four organic bases called adenine, thymine, guanine, and cytosine, shortened to A, T, G, and C. The full structure of each base is shown below, but this figure is only comprehensible to a biochemist, which I certainly am not! However, it is interesting to note that only four elements are present: Carbon (C), Oxygen (O), Hydrogen (H), and Nitrogen (N), which means that life evolved in all its complexity from a random chemical “soup” of those elements, which must make it the most extreme example of going from randomness to complex information (or from high to low entropy).
From Linus Pauling – General Chemistry
However, information theorists are not interested in the chemistry of DNA at this level. Rather, they are interested in the fact there are only two permissible pairs of connections between the four bases in the strands of DNA: A-T and G-C., imposing constraints on the information mechanisms. Thus, a very long string of almost random looking letters will bond only with an equally long string of letters, but only in a certain sequence. This allows the DNA to break up and form new chains, hence replicating life. This is shown in the figure below, taken from my first year physics book Mechanics by Charles Kittel, Walter Knight, and Malvin Ruderman.
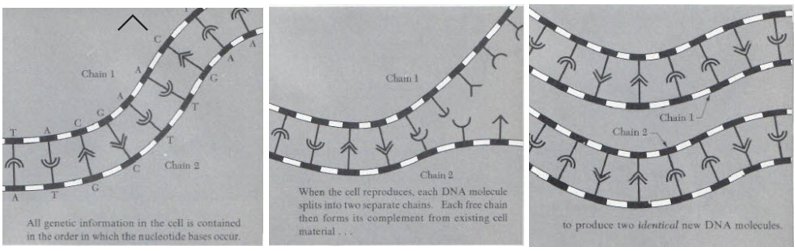
A visual explanation of the replication of DNA in creating life (Kittel, Knight, and Ruderman, 1962)
Therefore, modern information theorists are now working with the alphabet of life, which is rich in puzzles even more compelling than guessing a card correctly.
[1]Claude Shannon, 1948, A Mathematical Theory of Communication (7. The Entropy of an Information Source)
(Brian Russell – BIG Media Ltd., 2021)



Hi Christa,
I haven’t come up with an exact solution yet, but I would say that you could set up the problem as follows. Let W = the number of women in Calgary (actually, you could reduce the number if you knew the ages of all three of you. That is, the number of women between the ages of the oldest and youngest of you. But I won’t go there!). Let R = the number of women in Calgary with red hair. Then the probability of encountering a woman with red hair would be R/W. Now, your son has three women care-givers in his life. So the probability of picking those three women at random in Calgary would be 3/W (or is it? I’m not entirely sure about this.). The probability those 3 women having red hair is some combination of those two probabilities. It could be the product, but I’m not sure. I will think more about it, and perhaps someone else will weigh in with an idea. I’m not sure if entropy enters into it.
Brian
Hi Christa,
Sorry for not noticing this sooner. Let me think about it and get back to you.
Brian
I love these types of quizes as well but after a couple incorrect answers (a real blow to the ego), i now always assume there is some rule i’m forgetting about. Anyhow, i have a puzzle that you may be interested in solving. Last week, I was dropping my son off to preschool and noticed something quite intriguing. He attends two session of preschool. One is on M, W and Friday, another is on T and Thursday. In both sessions, his teacher has red hair. His mother also has red hair. What are the chances that all three caregivers in my sons life have red hair in Calgary? Can entropy theory be applied to this problem? The more i think about it, the more complicated it gets.