(Note from the editor: this article is not for everyone. If you have a background in science/mathematics, you will enjoy reading on. If, like me, you are not a scientist but enjoy reading about scientific issues presented in non-technical format, you will be better off reading this version of Brian’s article: Bridging the two cultures .If any of you science nerds have anything to add, we welcome your feedback in the comments section beneath the article.)
Introduction
Thermal physics is a branch of science that is at the intersection of chemistry and physics; the chemists calling it thermodynamics and the physicists calling it statistical physics. The beauty of the twin subjects of thermodynamics and statistical physics is that they solve the same problem in completely different ways. Although both subjects can get extremely complex, I am going to illustrate these two approaches using a simple problem, one that can be solved intuitively.
The problem
Let’s start with the basic problem I want to solve. This problem is illustrated by the following figure, which shows a group of 10 moving particles (they could be marbles, billiard balls, or gas molecules) constrained in a box and bouncing off the walls and each other. Notice that the box is divided into two halves by a moveable partition, and the particles are initially only in the left side of the box.
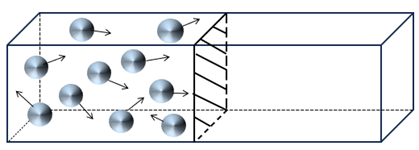
Figure 1 – Ten molecules trapped in the left half of a box by a partition.
What happens when we remove the partition? For a brief instant, the particles will remain in the left half of the box, but very quickly they will redistribute themselves over the full box, which is twice as large as the initial box. Intuitively, I think you will agree that the most probable situation is as shown below, with five particles in the left half and five particles in the right half. With 10 particles in total, this will not always be the case, and the two sides might have unequal numbers at any given time. But, as we add trillions of particles (i.e., molecules of gas), half of the particles should be in the left half of the box and half in the right side of the box (not the same particles, of course, since they are constantly moving).
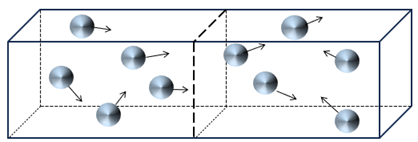
Figure 2 – The situation shortly after the partition in Figure 1 has been removed.
Now comes the amazing thing. This intuitive observation can be proved exactly in two ways, both macroscopically (by looking at things such as the volume of the box, the pressure exerted by the gas molecules, and the temperature of the gas) and microscopically (by looking at the number of molecules and their amount of disorder).
The thermodynamic solution
The science of thermodynamics evolved through the study of gases and the realization that the behaviour of gases could be summarized by a single law, called the perfect gas law, which was initially written
where P is the pressure exerted by the molecules of the gas, in Pascals, or kg/(m x s2), V is the volume enclosing the gas, in m3, T is the temperature of the gas, in degrees Kelvin, or K, n is the number of moles of gas, and R is called the universal gas constant, with the value
where J is energy in Joules. One thing that isn’t always mentioned is that P multiplied by V gives us an energy term. This can be seen by computing the units, which are in kg x m2/s2, or by noting that when R is multiplied by n moles and T, the mole and K terms are cancelled in equation 2, leaving just the Joule term.
Equation 1 is the way in which chemists like to express the perfect gas law, but physicists prefer a different formulation that explicitly includes the total number of molecules. To derive this formulation, note that a mole of gas has Avogadro’s number of molecules, NA, which is written 
Therefore, n moles of gas contain N = n x NA molecules, and we can re-write equation 1 as
where k is called Boltzmann’s constant and can be written as a function of Avogadro’s number and the gas constant as
where k is in energy units since temperature in degrees Kelvin is unitless. The ideal gas law in the form of equation 4 tells us that the pressure of the gas is inversely proportional to the volume of the gas and linearly proportional to both the number of molecules and the temperature.
In the macroscopic, or thermodynamic, approach, first note that equation 4 can be re-written for pressure as
Next, we introduce the concept of work, W, which is the integral of pressure with respect to the volume, from the initial volume, Vi, to the final volume Vf :
Equation 7 is difficult to solve if either N or T are a function of volume, but we are going to make the simplifying assumptions that N and T are constant. By keeping T constant, we are assuming what is called an isothermal expansion of the gas, and by keeping N constant we are assuming that no diffusion of the molecules is taking place. This makes sense in the above problem, since we don’t expect the temperature of the gas to change much when we open the partition, and we certainly are not going to lose or gain any molecules. This allows us to solve equation 7 as follows
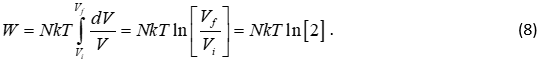
In the result we note from Figures 1 and 2 that the final volume is twice the size of the initial volume.
Next, let’s consider the first law of thermodynamics, which tells us that
where Q is the amount of heat, DU is the change in energy and W is the work. Note that some authors (e.g., Schroeder, 2021) use a negative sign for work, but others express the first law as shown above (e.g., Halliday, Resnick, and Walker, 2001). This simply depends on whether we define work as a compression or expansion, and I will use the above formulation as it will lead to a simpler derivation in what follows. Equation 9 can be simplified for an isothermal expansion, since there is no change in energy, leading to the following expression for heat in our problem:
Next, we recall the thermodynamic definition of entropy, which is
where DS is the change in entropy from its initial state Si to its final state Sf. However, for our problem, T is constant, leading the simple result
Note that entropy is in energy units since T is dimensionless, and that equation 12 gives us an amazingly simple result for our problem where N = 10, which is that the change in entropy from the initial state in Figure 1 to the final state in Figure 2 is equal to
which is a very small number if we look at the definition of k in equation 5. But, if the number of particles reached 10+23, as in a typical gas, the change in entropy would be roughly equal to 6.93, Joules/degree Kelvin.
The statistical physics approach
Now, let’s see if we can reproduce the results in equation 11 using the microscopic, or statistical, approach of statistical mechanics. In fact, it will be much simpler than the approach we have just taken. We start with Boltzmann’s famous expression for entropy (which is engraved on his tombstone), which is written
where S is again the entropy, k is again the Boltzmann constant, and Ω is the number of configurations for the N molecules in the gas. To make this equation look more like equation 11, let’s consider the change in entropy using the initial and final states, or.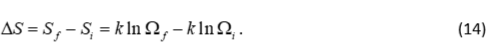 
All that is left to do is calculate Ωf and Ωi, which can be done using the following equation
where we note that n goes from 0 to N and is not the same as the term we used earlier to define the number of moles. In other words, if n is the number of molecules in one side of the box in Figure 2, then N – n is the number of molecules in the other side. The following table shows the number of configurations versus n:
Table 1 – The number of configurations for N = 10 particles in a box, where n equals the number of particles in the left half of the box (see Figures 1 and 2).
As expected, the number of configurations is symmetric around n = 5 = N/2. To understand how these computations were made, let’s apply equation 14 to the first and last three calculations:
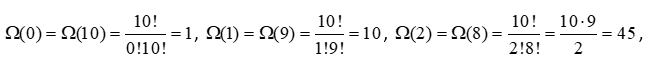
and so on for the other five calculations. If we add all the configurations together, we get 210 = 1024 possible configurations. To see why, consider N = 2, 3, and 4 particles and extrapolate to N = 10. If we divide the values in Table 1 by 1024, we get the probability of finding a certain configuration, where the sum of the probabilities is equal to 1. Here are plots of the results:
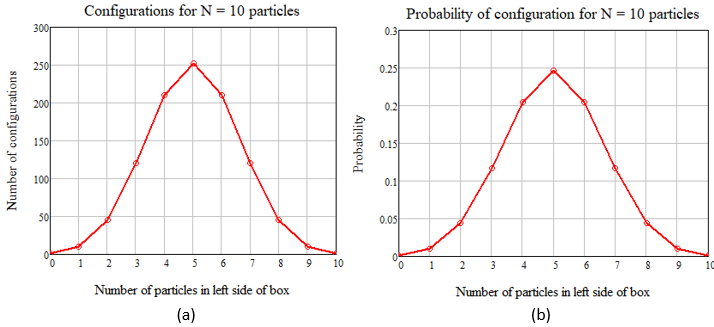
Figure 3 – A plot of the results in Table 1, where (a) shows the total number of configurations and (b) shows the probability of n particle on the left half of the box.
Next, let’s let N = 100. Here is a plot of the results, both in total configurations and probability format:
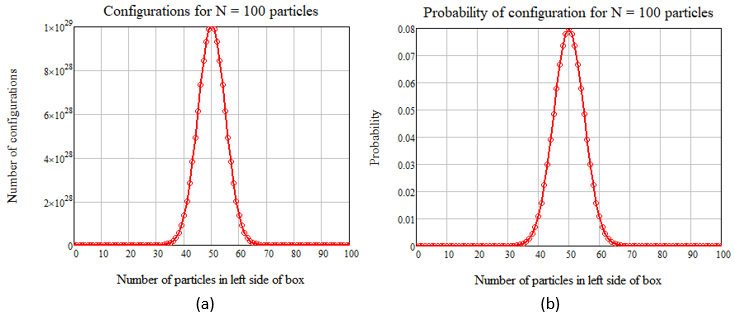
Figure 4 – The same as Figure 3, but with N = 100, where (a) shows the number of configurations and (b) shows the probability of n particles in the left (or right) side of the box.
If you compare Figures 3 and 4, you can see that the plots on the right-side approach a Gaussian probability distribution, which is proved theoretically in chapter 1 of Reif (1965). As N gets larger, the maximum on the Gaussian curve approaches 1, and the width approaches zero, a true delta function. But, if you look at the un-normalized curve in Figure 4(a), you will see that for N = 100, the number of configurations for the most probable situation of n = 50 is equal to 1029, a huge value. As we approach Avogadro’s number of molecules, this value tends to infinity. In fact, for this many molecules we are justified in ignoring all the configurations that are not at n = N/2, since they are vanishing small compared to the central value. This allows us to use Stirling’s approximation for the factorial of N, which is written
We can now compute the entropy change from equation 14. For the initial configuration shown in Figure 1, we see that
If we assume that N is much larger than 10, we can assume that only the maximum configuration contributes to the final state, so that we write
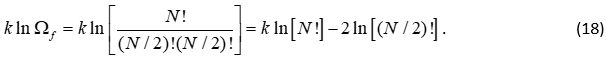
Next, we use Stirling’s formula to get
Combining equations 17 and 19 gives
Notice that equation 20 is identical to equation 12 but was derived using a completely different method!
Conclusions
In this tutorial, I compared the two branches of thermal physics – thermodynamics and statistical physics – using a simple problem, one that can be solved intuitively. The problem involved a group of 10 moving particles that were initially confined in the left half of a box that was divided into two halves by a moveable partition. These particles were bouncing off the walls and each other. We then opened the partition and waited until the particles had a chance to spread over the whole volume of the box. Intuitively, we felt that the final configuration would approximate five particles in each half of the box.
We then computed the change in entropy between the initial configuration and the final configuration using classical thermodynamics, which assumed only the volumes of the box before and after the partition was removed, the total number of particles, the ideal gas law, and the first and second laws of thermodynamics. Next, we computed the change in entropy using Boltzmann’s approach, which only assumed most probable configuration of the initial state and the final state. Amazingly, we got the same result using both assumptions.
References
Halliday, D., Resnick, R., and Walker, J., 2001, Fundamentals of Physics, 6th Edition: John Wiley & Sons, Inc.
Reif, F., 1965, Fundamentals of Statistical and Thermal Physics: McGraw-Hill Inc.
Schroeder, D.V., 2021, An Introduction to Thermal Physics: Oxford University Press.
