Brian Russell (middle) jamming in Plaza Santa Ana, Madrid, in 2018. (Photo by Natasha Hunt)
In the first part of this series – Music, mathematics, and physics – I explained why we have 12 notes in western music. In Part 2 – Music, mathematics, and physics Part 2 – musical scales – I looked at scales, which is the way these 12 notes are grouped together. In this third article, I will discuss harmony and chords, the creation of music that involves playing two or more notes together at the same time. This is a topic dear to my heart, as I love playing chords. My fellow Canadian geophysicist and guitar player David Lumley jokingly calls me “Guitar George”, from a line in Sultans of Swing by Dire Straits (“You check out Guitar George, he knows all the chords”).
I will again start with the circle of fifths (clockwise) or fourths (counterclockwise), as illustrated below:
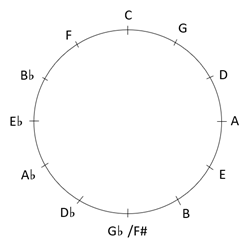
You will recall from Part 2 that any three consecutive letters in a clockwise direction consist of the subdominant, tonic, and dominant notes of a musical scale. If C is the tonic, it is the first note in the C scale, F is the fourth note, and G is the fifth note. I also discussed musical intervals, which consist of playing two notes at the same time (i.e. the tonic and dominant create a fifth interval).
In ancient Greek music and European music for the first millennium AD, music was largely monophonic, consisting of single notes either sung or played on an instrument. In the second millennium, as discussed by Donald Jay Grout in his book A History of Western Music, music became polyphonic, where several notes were sung or played simultaneously. This was largely inspired by sacred music in the Roman Catholic church. In early polyphonic forms such as organum and the motet, strict rules had to be adhered to. It was believed that God had decreed only three perfect intervals; the octave, fourth, and fifth. Therefore, these were the only intervals that were allowed.
As time progressed through the Medieval, Renaissance, and Baroque musical eras, these rules were gradually relaxed and polyphony involved up to four notes played together using intervals of a third, as well as the fourth, fifth, and octave. This is called four-part harmony and consists of the four “voices” – soprano, alto, tenor, and bass, which were either actual voices or played on different instruments, as in a string quartet. Although called four-part harmony, the basic structure consisted of three-note chords, or triads, of which one note would be doubled. The next figure shows the 14 triads found by adding two-thirds to each note in both a C major scale and C harmonic minor scale. The C harmonic minor is in the key of E♭ major with three flats, where B♭ is raised to B (shown by the natural sign ♮ in the figure):

(a) C major (b) C Harmonic Minor
The harmonized C scales.
There are four types of triads shown here – major, minor, diminished, and augmented (the augmented triad only appears in the minor scale). The notation for the triads is shown in two ways, at the top and bottom of the staff. At the top, the major triads are written as the names of their tonics, but the minor triads are followed by “m”, indicating minor. The diminished triads are written with a o superscript and the augmented triad with a + superscript. At the bottom, capital Roman numerals indicate the major or augmented triads, and small Roman numerals indicate the minor triads, where the numerical value indicates the relative position of the chord within the scale. The Roman numerals allow us to generalize the triads for every key signature.
But what gives each triad its unique sound? First, notice that major and minor triads all have an interval of a perfect fifth between the first and third note, but the major triads have a major third as the first interval, and the minor triads have a minor third as the first interval. (A major third is separated by two full tones, and a minor third is separated by one-and-a-half tones). The diminished triad has a minor third interval between the first two notes, but has a flatted fifth interval between the first and third notes. To make this clearer, here is a figure showing the four forms of the C triad:

The four C triads.
Why not add a fourth note to the chord using another third, which would be the seventh note of the scale? In classical harmony, a seventh is often added to the dominant chord. In the case of C major, this would mean we create a G7 chord by adding an F above the D (that is G-B-D-F). In my last article, you will recall that F is not actually in the key of G, since the G scale contains an F#. Therefore, in the key of G, the F note would be called a flatted seventh. This is called a dominant seventh chord, or V7, in classical harmony, and can be built from the dominant in each key.
Using the Roman numeral notation now allows me to make a very bold statement. Virtually every song you have ever heard in western music – from nursery rhymes, to the classical repertoire, to rock, and country music – is probably based on the I, IV, and V (or V7) chords in major keys, and the i, iv, and V (or V7) chords in minor keys. For example, the only chords you need to know to play Twinkle Twinkle Little Star are C major, F major, and G7, the I, IV, and V7 chords in the key of C major. Here are those three chords on the guitar, ukulele, or piano, allowing you to play it to your child or grandchild:
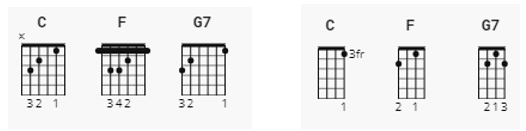
(a) Guitar (b) Ukulele

(c) Piano
Chords to Twinkle Twinkle Little Star (from Ultimate-Guitar.com).
In classical music, the chords are slightly more disguised, but virtually all classical pieces of music involve some combination of I-IV-V in major keys or i-iv-V in minor keys. Let’s look briefly at one of my favourite pieces, the Bourrée from Bach’s Lute Suite in E minor. (Be sure to listen to Julian Bream playing on the classical guitar). Even though Bach wrote the piece using two-note polyphony, or counterpoint, you can clearly hear him modulating between i and V in E minor throughout the piece, or E minor to B major. Ian Anderson of Jethro Tull does a wonderful transcription of the Bourrée where he first plays it with bass and flute as the two voices, then follows up with a jazz/rock version where a rhythm guitar plays the underlying chords. Anderson plays the piece to the key of D minor, meaning that it now modulates between D minor and A major. This shows the advantage of the Roman numeral notation, which is independent of the key signature.
The i-V modulation is also central to much gypsy and folk music. One of my musical highlights was being invited to play with two street musicians in Madrid (see the opening photo and THIS YOUTUBE link), after I told the guitarist in my broken Spanish that I owned the same model Ramirez guitar as him. Being put on the spot, I started alternating between an A minor and E major chord (i-V in the key of A minor), and the accordion player spontaneously played an amazing solo.
Let’s now look at a quick sample of music from the late 20th century that we are all familiar with, from the Everly Brothers, to Bob Dylan, and the Beatles. If you analyse the structure of their songs, many of them are based around I, IV, and V in various keys. Here is my analysis of some of the most well-known songs of the last 60+ years:
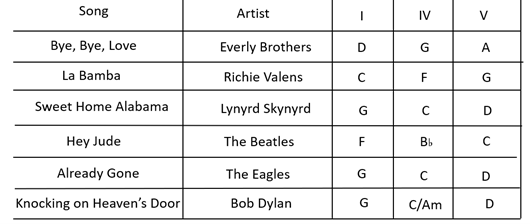
Once in a while, there is a surprise, as when Bob Dylan alternates C with Am throughout Knocking on Heaven’s Door. But remember that Am is the related minor to C major, so your ear is happy with the substitution.
But the strict rules of classical music and simplified rules of rock and roll were meant to be broken, and this is where blues and jazz come in. For example, 12-bar blues is built on the I, IV, and V chords of a given key, but now add a flatted seventh to each chord. Since only the V7 would be allowed in classical music, this gives the blues a different sound. In its most common form, 12-bar blues is as follows, where each bar usually consists of 4 beats, and each chord is a dominant seventh:
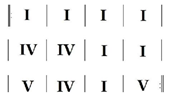
The 12-bar blues in Roman numeral form.
If you combine the 12-bar blues with a knowledge of the minor pentatonic scale, which I discussed in Part 2, and work hard, you might get a gig in a blues club, once the pandemic is over. Many famous rock songs – including Mustang Sally – are also based on the 12-bar blues.
There are many variations on this basic pattern, especially when the blues is played by a jazz musician. This brings me to my final topic – jazz, where things really go crazy with seventh chords! In the figure below, a seventh has been added to every triad in the C major scale. On the top are the names of the chord in the key of C, and at the bottom its equivalent Roman numeral.

The jazz sevenths in C.
There are now four types of sevenths – the major sevenths (Cmaj7 and Fmaj7), the dominant seventh (G7), the minor sevenths (Dm7, Em7, and Am7), and the half-diminished seventh (BØ7, also called B7♭5). (There is also a full diminished seventh, where each note is a minor third apart, but I won’t discuss it in this article). The major sevenths and dominant sevenths are built from the major triads, the minor sevenths from the minor triad, and the diminished seventh from the diminished triad. For the major sevenths, the seventh note is a semitone from the root, but for all the rest it is a full tone from the root. What sets jazz apart from other music forms is its liberal use of these seventh chords.
The most common use of these chords is in what is called a ii-V-I, which in C major consists of Dm7-G7-Cmaj7. Looking at the circle of fifths, you will see that this sequence uses any three consecutive chords in a counterclockwise direction around the circle (that is, three consecutive fourths). An example of this is the song Giant Steps by John Coltrane, given this name because it uses the ii-V-I sequences taken from three “giant steps” around the circle of fifths, starting on B. The first step is C#mi7-F#7-Bmaj7, the second step is Ami7-D7-Gmaj7, and the third step is Fmi7-B♭7-E♭7, and you will see that the major keys of B, G, and E♭ are exactly four steps apart on the circle of fifths, dividing it into three equal parts. As a less esoteric example, the song I’ve Got Rhythm by George Gershwin, called Rhythm Changes by jazz musicians, is based around the sequence Cm7-F7-B♭maj7. Countless songs have been based on these chord changes, the best known one being the theme to The Flintstones!
I hope you have enjoyed this three-part “tour” through music and science. Feel free to add to the discussion in the comments below.


