Prisoner’s dilemma and vaccination

The last 18 months have felt like a prison sentence for many of us. Therefore, it seems appropriate that we look at how a famous problem in game theory known as prisoner’s dilemma might relate to our current challenges. Prisoner’s dilemma[1]presents a scenario in which the choice of action can bring about a result that is great for one prisoner and terrible for the other, reasonably good for both parties, or bad for both parties.

Two criminals (A and B) have been arrested and placed in solitary confinement. They each have an important decision to make independently, and they may act co-operatively, punitively, or selfishly. Here is the situation and their choices:

• There is insufficient evidence to convict each of them with the greater crime, which carries a sentence of three years in prison.
• Enough evidence exists to convict them both of a lesser crime, which carries a sentence of one year.
• The prosecutor offers each prisoner a deal: to betray the other prisoner and serve no time.
• They can choose to stay silent.

The outcomes are:

• If A and B each betray each other, they each serve a two-year sentence
• If A betrays B but B remains silent, A will be released, and B will serve three years in prison.
• If A remains silent, but B betrays A, A will serve three years in prison, and B will be released.
• If A and B both remain silent, both will serve one year in prison.

Choosing to be vaccinated for COVID-19 or not is both like and unlike this problem, though prison sentences are not part of the scenario at this time. In fact, the decision to vaccinate against any disease has long been discussed as a problem in game theory.[2] Individuals choose to vaccinate or not based on the cost of vaccination and the perceived risks of the disease and the vaccine, as well as related factors. Moreover, co-operation may be an important factor in the decision to receive a COVID vaccine or not.

New information and the dilemma

The prisoner’s dilemma presents more than one way to evaluate a “good” choice. Two of them are:[3]

• Purely self-interested prisoners will betray their partners if they assume there will be no future punishment in their criminal fraternity for doing so. This has the highest individual reward.
• Purely co-operative prisoners will stay silent. The average punishment will be less than any other solution.

But what if new information is added, such as an iteration of the game or knowledge of the other player’s likely choices?[4]

Matters can become more complex, and more like the vaccination question in which the populace’s vaccination status may be known, and the understanding of the cost-reward variables may be updated. The possibility of vaccine passports for international and even regional travel, along with the higher level of infectiousness of the COVID-19 Delta variant, and the level of vaccine effectiveness against Delta, may all affect the decision.

The latest relevant information

Vaccine passports, or proof of vaccination against COVID-19, is as pervasive a topic as the disease itself. While numerous states with the United States currently ban vaccine passports or do not require them, other jurisdictions in the world, including parts of Canada, will require proof of vaccination for air travel.[5]The European Union has a digital passport system available to all 27 member nations that may be used to avoid testing or quarantine.[6]Where vaccine passports are used, how they are used, and how they are perceived will continue to evolve.

In a recent report by BIG Media Understanding vaccine effectiveness and breakthrough, the Delta variant basic reproductive rate, or Ro, was reported to be between 5 and 9.5.[7]

In another BIG Media article Predicting vaccination rates and outcomes for the Delta variant, Big Media, vaccine effectiveness was taken into account for the herd immunity vaccination rate. It was shown that the herd immunity vaccinate rate is affected by vaccine effectiveness (E) in the following way:

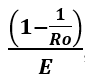
Any vaccine effectiveness less than 100% increases the herd immunity vaccination rate. For the Delta variant, an effectiveness of 80% or greater may be required for herd immunity to be possible.[8]

Previous studies of vaccinations and game theory

The study of vaccination in terms of game theory has been researched extensively. The idea of maximizing utility (self-interest) versus the greater good was examined for influenza vaccination.[9] This work and similar studies lay the groundwork for our understanding of the framework around the COVID vaccination question.[10]The game theoretic strategy for a person considering vaccination follows a quantitative payoff formula that uses these variables:

• The probability of infection for an unvaccinated person, π_v
• The perceived ratio of morbidity (m) from being vaccinated (m_v) versus infected (m_i), where m = m_v / m_i. This term is not the same as vaccine effectiveness because it considers the risk of the vaccine itself. Morbidity means a state of disease. In this case, either significant side effects from the vaccine or symptomatic illness from infection.
• The basic reproductive rate (Ro)
• Vaccine effectiveness (E)
• The vaccination rate (v)
• Costs of being vaccinated, including time, money, and inconvenience

One of the key differences between the classic prisoner’s dilemma and the vaccination problem is that, for vaccination, individuals have knowledge of what others are doing statistically. For example, the vaccination rate is known.

The argument is strongest for vaccination when the probability of infection is high, when Ro is high, when perceived vaccine effectiveness is high, when the ratio of morbidity is low, when perceived side effects and costs are low, and when the vaccination rate in the population is low. The table below summarizes some of these variables.

Table summarizing the utility to vaccinate. Some variables increase utility as they increase in value, and others decrease utility as they increase in value. The inverse relationship between vaccination rate and utility is an issue in eradicating any disease. The perceived ratio of morbidity, which is a relative risk measure, is crucial in game theoretic analysis of vaccination.[11]

Game theory is mathematical in nature. The starting point for a strategy centres on the probability that an individual will choose to vaccinate (P) and the payoff of such a choice.

Payoff (PAY) to vaccinate at a probability (P) and a vaccination rate (v) is:

PAY (P,v) = P(-m_v) + (1 – P) (- m_i π_v)  and since m = m_v / m_i.

PAY = -mP  – π_v (1 – P)  [12]

There is a complex interaction between vaccine risk (ratio of morbidity), vaccination rate, probability of infection (π_v), and Ro (as it affects π_v) on the game theory utility of being vaccinated.

In fact, as v approaches  the incentive to vaccinate lowers because π_v lowers.

1. The effect of the perceived ratio of morbidity (which is a relative risk measure) is also important. If the vaccine safety is questioned and this ratio becomes higher than 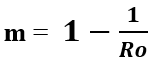 then vaccination programs are unlikely to succeed. Any perceived risk of vaccination (i.e. any non-zero value for m) has been argued as making disease eradication unlikely.[13]

A demographic problem

The game theoretic study of influenza vaccination programs showed a demographic issue. Influenza is primarily transmitted in younger people and working adults, but influenza is generally more deadly to older individuals. Optimal vaccine strategies for influenza would target younger people to most efficiently stop spread, but, from a game theory perspective, there is less utility in these younger people choosing to be vaccinated. This is a conflict between rational self-interest and the greater good.[14]

This problem exists for COVID-19 for the same reasons. Younger adults have less utility in being vaccinated, and children under 12 years old are not approved for vaccination.

Game theory arguments for the present situation

The Delta variant having a high Ro value increases the utility for vaccination.

The likelihood that herd immunity may be difficult, or even impossible, to achieve for the Delta variant could have two opposite effects on the utility of vaccinating. Possibility 1 is the argument that if the disease cannot be eradicated, the probability of infection (π_v) remains non-zero, and there is a continuing reason to be vaccinated. Possibility 2 is that if confidence in the vaccine effectiveness is lowered, the perceived utility of vaccination is eroded.

There is a conflict between individual utility and the greater good in the vaccination choice for younger adults as none of the vaccines is approved for children.

Ongoing concerns for vaccine safety are crucial in game theory analysis. This is both a rational and factual issue, but it is also an issue of public perception. On August 23, 2021, the United States Food and Drug Administration approved the Pfizer COVID vaccine, though it is still not approved for children under 12 years old.[15]

The cost of not vaccinating increases with the use of vaccine passports. This may increase the utility of vaccinating for those affected by the rules relative to the passport. Such requirements must be considered carefully since societal co-operation remains important in eradicating any disease.

Interpretation

The choice to vaccinate is both alike and unlike the prisoner’s dilemma. In both cases, individuals are affected by the choices of other individuals, and co-operation (or the greater good) must be weighed against rational individual self-interest. In the vaccination case, knowledge of the choices of others, such as in vaccination rates and the changing probability of infection as these rates increase, is a factor.

The effects of recent events such as the Delta variant’s higher infectiousness could have various consequences, but other issues are clearer. The perceived safety of any vaccine is crucial in its uptake. This is an ongoing, but more predictable issue for governments. The approval of vaccines for children is another key issue that may have been predicted and acted upon differently.

Eradicating any disease is unlikely purely from the game theoretic perspective of individual self-interest, which is why public perception, and the degree of societal co-operation are important. Any new measure must be considered from both an ethical perspective and how it might affect the level of co-operation within the population. The utility of vaccine passports has a mathematical argument on utility in its favour, but its effect on co-operation remains to be seen.

Would you throw the other prisoner under the bus and take the risk that comes with the highest personal reward, or would you seek to co-operate with the other party in order to help produce a result that is relatively good for both prisoners?

References

[1] Poundstone, William, 1993, Prisoner’s Dilemma: John Von Neumann, Game Theory and the Puzzle of the Bomb, Knopf Doubleday Publishing Group

[2] Bauch, Chris, David Earn, 2004, Vaccination and the theory of games, PNAS, Vol.101, No. 36, 13391-13394

[3] Poundstone, William, 1993, Prisoner’s Dilemma: John Von Neumann, Game Theory and the Puzzle of the Bomb, Knopf Doubleday Publishing Group

[4] Milovsky, Nicholas, Sept 10, 2013, The Basics of Game Theory And Associated Games

[5] Panettieri, Joe, August 16, 2021, United States, Europe, Asia and More Vaccine passport policies, Channele2e

[6] BBC News Explainers, August 6, 20221, The EU vaccine ‘passport’ and what it means for travel

[7] Hunt, Lee, August 3, 2021, Understanding vaccine effectiveness and breakthrough, Big Media

[8] Hunt, Lee, August 16, 2021, Predicting vaccination rates and outcomes for the Delta variant, Big Media

[9] Galvani, Alison, Timothy Reluga, Gretchen Chapman, 2007, Long-standing influenza vaccination policy is in accord with individual self interest but not with the utilitarian optimum, PNAS, Vol.104, No. 13, 5692-5697

[10] Bauch, Chris, David Earn, 2004, Vaccination and the theory of games, PNAS, Vol.101, No. 36, 13391-13394

[11] Bauch, Chris, David Earn, 2004, Vaccination and the theory of games, PNAS, Vol.101, No. 36, 13391-13394

[12] Bauch, Chris, David Earn, 2004, Vaccination and the theory of games, PNAS, Vol.101, No. 36, 13391-13394

[13] Bauch, Chris, David Earn, 2004, Vaccination and the theory of games, PNAS, Vol.101, No. 36, 13391-13394

[14] Galvani, Alison, Timothy Reluga, Gretchen Chapman, 2007, Long-standing influenza vaccination policy is in accord with individual self interest but not with the utilitarian optimum, PNAS, Vol.104, No. 13, 5692-5697

[15] Food and Drug Administration, August 23, 2021, FDA Approves First COVID-19 Vaccine