My granddaughter is in her second year of physics and geophysics at UBC, and one of the courses she is taking this semester is titled Thermal Physics. This is a branch of physics I really enjoyed when I was studying at the University of Saskatchewan over 50 years ago, so I decided to buy her textbook of the same name, by Daniel Schroeder, and re-study the subject myself, both for fun and in case she asked for help in any of her assignments.
As I studied the book, I realized that there are lessons to be learned from this area of physics that should be of interest to non-scientists in this time of skepticism about science and scientists. First, thermal physics was developed over several hundred years by a few brilliant individuals and is therefore interesting from a historical perspective. Second, thermal physics is fundamental to the study of the Earth’s climate, and, regardless of your position on the great debate (Climate change and energy: context for the great debate), rest assured there are many good scientists tackling complex issues related to climate change. Thermal dynamics is also fundamental to topics as diverse as the study of engines and refrigerators in engineering, and complex metabolic processes in biochemistry.
Thermal physics is at the intersection of chemistry and physics, the chemists calling it thermodynamics, and the physicists calling it statistical physics. The beauty of the twin subjects of thermodynamics and statistical physics is that they solve the same problem in completely different ways. I can illustrate these two approaches using a simple problem that can be solved intuitively. This problem is illustrated in the following figure, which shows a group of 10 moving particles (they could be marbles, billiard balls, or, more importantly, gas molecules) constrained in a box and bouncing off the walls and each other. Notice that the box is divided into two halves by a moveable partition, and the particles are initially only in the left half of the box.
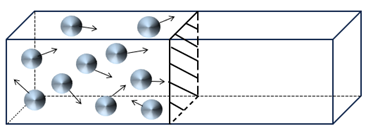
What happens when we remove the partition? For a brief instant, the particles will remain in the left half of the box, but very quickly they will redistribute themselves over the full box, which is twice as large as the initial box. Intuitively, I think you will agree that the most probable situation is as shown below, with five particles in the left half and five particles in the right. With 10 particles in total, this will not always be the case, and the sides might have unequal numbers at any given time. But, as we add trillions of particles (i.e., molecules of gas), half the particles should be in the left half of the box and half in the right side of the box (not the same particles, of course, since they are constantly moving).
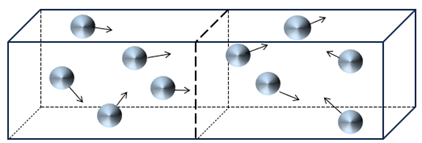
Now comes the amazing thing. This intuitive observation can be proved exactly in two ways, both macroscopically (by looking at things like the volume of the box, the pressure exerted by the gas molecules and the temperature of the gas) and microscopically (by looking at the number of molecules and their amount of disorder).
The macroscopic viewpoint, called thermodynamics, was developed over several hundred years by scientists including Robert Boyle (Irish, 1627-1691), Jacques Charles (French, 1746-1823), John Dalton (English, 1766-1844), Amedeo Avogadro (Italian, 1776-1856), and Joseph Louis Gay-Lussac (French, 1778-1850).
The microscopic viewpoint, called statistical mechanics, was developed more recently by James Clerk Maxwell (Scottish, 1831-1879), Josiah Willard Gibbs (American, 1839-1903), and Ludwig Boltzmann (Austrian, 1844-1906), 
Ludwig Boltzmann (from Wikipedia)
But here is the rub. I wanted to provide you with the derivation of these two approaches so you could see how wonderful science is. However, as I proceeded, I discovered that the process was not as easy as I thought it would be. It involved introducing physical ideas such as the ideal gas law, the first and second laws of thermodynamics, the concept of entropy, and the mathematics of logarithms and factorials. Not the kind of stuff you want to see in an article for non-scientists (although it may have been of interest to readers who have some background in chemistry, physics, and mathematics). But, if you will permit me one equation, the result of both approaches can be expressed simply as follows:
![]()
where DS is the increase in entropy, or disorder, of the molecules, and k is a very small number (approximately 10-23) called Boltzmann’s constant. More specifically, 6.93 is the product of 10 (the number of particles) and the natural logarithm of 2 (the logarithm of the increase in volume between the first and second figure), so if the number of particles reached approximately 10+23 (called Avogadro’s number), as in a typical gas, the change in entropy would be roughly equal to 6.93, with units of Joules/Kelvin, a measure of energy divided by absolute temperature.
This exercise taught me that although many scientific concepts can be very intuitive (as with the example above), deriving the results requires a completely different mindset and set of tools, usually mathematical. This has led us to the point where scientists are often looked on with skepticism and mistrust by the general non-scientific population, which is an unfortunate situation, given how dependent our society is on scientists in areas such as technology and medicine (not to mention pandemics and climate questions).
The uneasy relationship between scientists and non-scientists is not a new phenomenon. It was addressed by C.P. Snow in a 1959 lecture titled “The Two Cultures and the Scientific Revolution”, which inspired the headline of this article. The writing is a bit dated and is centered around the Oxbridge (Oxford and Cambridge) intellectual elite of the time, but Snow makes several very important observations in his lecture, which ring true to this day. (I was able to buy it for about $2 as an e-book from Amazon.)
Snow’s first observation was that there existed a snobbery on the side of both the non-scientists and scientists about the other group, the scientists expressing contempt about how little non-scientists (whom he called literary intellectuals) knew about science, and the non-scientists expressing contempt about how little scientists knew about literature and the fine arts. He sums this up by relating a story that I will paraphrase, and which pertains very much to the subject of the first part of my article.
He talks about being with a group of literary intellectuals who were bemoaning the lack of cultural knowledge of scientists, and he asked them how many of them know the second law of thermodynamics. None of them had the faintest clue. He pointed out that this was the equivalent of never having read a play by Shakespeare, in literary terms. He went on to ask them how many understood the concept of mass, and only one in 10 knew. He pointed out that this was the literary equivalent of not knowing how to read!
Snow then ponders how we get around this problem of cultural miscommunication, because it would be of great interest to get the two cultures communicating with each other. He felt that the biggest obstacle was the over-specialization of the English school system, which meant that the literary elite knew much more literature than students from any other country’s school system, and the scientific elite knew much more science.
But the reverse was true: each specialist knew much less about other areas of knowledge than in other school systems. In North America, and in Canada particularly, we teach a broader range of subjects up to the end of high school, and even in university have less concentrated programs than in other countries. The result is that arts students in Canada often know more science than their counterparts in other countries, but still not to the level that they would need to follow new developments in science.
The next part of Snow’s lecture was concerned with comparing the strengths and weaknesses of the British, United States, and Russian school systems, and his conclusion was that each had strengths and weaknesses. He then looked at the effect of scientific knowledge on the disparity between the rich industrial nations and the poorer non-industrialized nations, which has continued to increase. One fascinating point is that Snow cites China as one of the least industrialized nations. Of course, since 1959, China has become one of the most industrialized and scientifically advanced nations.
Snow’s lecture was given long before the artificial intelligence revolution, and it is interesting to update his points for the new “two cultures”, those who develop and use the new machine learning technologies and those for whom these technologies are incomprehensible.
Again, it is incumbent on our school systems to adapt to these rapidly changing technologies and educate students about them. I suggest that we need a new way of educating our young people, with a much higher emphasis on learning the mathematics behind machine learning and science behind new research in such areas as quantum computing and biochemistry. Not that everyone must become a specialist, but that they should know enough to not be bamboozled by the new technology.
Likewise, we need to teach our science students more about language, history, and literature. The recent move toward schools that emphasize a more classical education is a good start. In any event, I would like to see a narrowing of the gap between the “two cultures” so that we return to a higher level of respect for scientists and their scientific advances.
Of course, skepticism, particularly when it is from an informed perspective, can be constructive and will always be an important aspect of good science, as fellow geophysicist Laurie Weston explains in her three-part series on fundamental principles of science; The scientific method: Science – there is method to the madness; Manipulating science – activism and advocacy; Science and morality – ethics and judgement.
By the way, for those who would like a more in-depth look at the inner workings of thermal physics, I have a more detailed discussion of the problem discussed earlier. For those who would like to read more about thermodynamics and statistical physics from a non-mathematical point of view, I highly recommend the book Einstein’s Fridge by Paul Sen, which was suggested to me by my long-time colleague Dan Hampson.
(Brian Russell – BIG Media Ltd., 2024)


